克莱因瓶被称为装不进水的瓶子，1874年德国大数学家克莱因设计了一个瓶子，它装不进水，当然也就卖不出去，不过这个克莱因瓶却使人们，特别是数学家大开眼界。

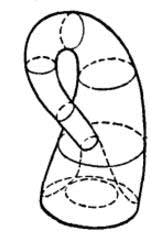
在数学领域中，克莱因瓶没有内部和外部之分，克莱因瓶最先是由德国数学家菲利克斯·克莱因提出的。克莱因瓶和莫比乌斯带非常相像。

还有一则科学幻想故事。故事的起因是有一个叫墨彼乌斯（M6bius)的数学家曾经制作了一个环（后人称其为墨彼乌斯环）。此环制作起来很简单，你不妨自己动手做一个：找一长长的纸条，在桌子上摊平，拿起一端，旋转180°,然后跟另一端粘合，就制成了。墨彼乌斯环的内壁和外壁是相通的，不信，你在你制作的墨彼乌斯环上涂抹一层糖浆，捉一只蚂蚁，放在纸条上让它顺着纸条爬，可以目睹它从外环爬到内环。墨彼乌斯环的环面不分里外，因此是二维的，可却放在三维空间中。设想墨彼乌斯环是透明的，环里画一头黑色的驴，让这头驴顺着环面前迸，转着转着，这二维世界的驴顺着墨彼乌斯环转一圈竟然颠倒过来了。如果你想像着小黑驴不离开纸面，原地旋转，使四蹄仍然朝下，小黑驴的头就朝向后方了：这表明，经过墨彼乌斯环前进一圈的小黑驴已从“左向驴”变成了“右向驴”!于是，就有人想像，若把墨彼乌斯环从二维推演到三维，会存在一个只有一个开口的瓶子。（根据推理,它是一只放在四维空间里的三维物体！）最早有个叫克莱因的人设想了这种空间，后人就把它称之为克莱因瓶。如果一个左心人钻进克莱因瓶转一圈，就会变成右心人！有人设想，我们所在的宇宙就是一个如同克莱因瓶那样的封闭的空间，如果从地球出发，到宇宙里去转一圈，左心人就会变右心人！

要使瓶子能够装水，必须有两个条件:第一，它盖上盖子后必须是封闭的，这是不言而喻的。一般人觉得这个条件就够了，在现实生活中也的确如此。可是克莱因说，单这个条件还不够，这个封闭曲面还必须是双側的，也就是这个曲面必须有里外之分，换句话说，水在里面不能跑到外面来。可是哪里有里外不分的瓶子呢?在莫比乌斯带的启发下，克莱因认为有这种可能性。  
克莱因的办法是从一个两头开口的管子出发，如果把管子两头弯曲，一直弯曲到两头相遇，然后把它们粘接在一起，这样就得到了一个环面。现在改变一个办法，先将管子一端弄得一端稍粗一些，一端稍细一些，这从拓扑上讲是容许的，它还是圆柱形。然后把两头弯曲，把细的一头插到粗的一头的管壁之内，然后两头从里面相接近,在接口处可以看到两个同心圆，大的一头套着小的一头，最后把小口放大，大口缩小，两口重合粘接在一起，这样得到的曲面如同环面一样也是封闭的。但是，它是单侧的，“外面”的一个小虫沿曲面爬，最后也可以爬到里面。

美中不足的是，克莱因瓶在三维空间中一定存在着自交点，只有到了4维空间，它才有一个正则的嵌入。

正如射影平面可以通过环面对顶点相粘合而成。克莱因瓶也可以通过球面对顶点相粘合而成。

我们可以把克莱因瓶沿着一条闭曲线剪开，这样我们就得到两条莫比乌斯带。因此，我们也可以把克莱因瓶看成二条莫比乌斯带沿公共边界相粘接而成，它的单侧性就更容易看出来了。

标签： 数学

咬字典百科 » 克莱因瓶，装不进水的瓶子与墨彼乌斯环
免责声明：本文由网友提供互联网分享，不代表本网的观点和立场；如有侵权请联系删除。